Reasoning by analogy in social science education: On the need for a new curriculum

I’d like to revisit the distinction between measurement models and statistical models. Rasch was well known for joking about burning all books containing the words “normal distribution” (Andersen, 1995, p. 385). Rasch’s book and 1961 article both start on their first pages with a distinction between statistical models describing intervariable relations at the group level and measurement models prescribing intravariable relations at the individual level. I think confusion between these kinds of models has caused huge problems.

We typically assume all statistical analyses are quantitative. We refer to any research that uses numbers as quantitative even when nothing is done to map a substantive and invariant unit on a number line. We distinguish between qualitative and quantitative data and methods as though quantification has ever been achieved in the history of science without substantive qualitative understandings of the constructs.

Quantification in fact predates the emergence of statistics by millennia. It seems to me that there is a great deal to be gained from maintaining a careful distinction between statistics and measurement. Measurement is not primarily performed by someone sitting at a computer analyzing data. Measurement is done by individuals using calibrated instruments to obtain immediately useful quantitative information expressed in a universally uniform unit.

Rasch was correct in his assertion that we can measure the reading ability of a child with the same kind of objectivity with which we measure his or her weight or height. But we don’t commonly express individual height and weight measures in statistical terms. 

Information overload is one of the big topics of the day. Which will contribute more to reducing that overload in efficient and meaningful ways: calibrated instruments measuring in common units giving individual users immediate feedback that summarizes responses to dozens of questions, or ordinal group-level item-by-item statistics reported six months too late to do anything about them?

Instrument calibration certainly makes use of statistics, and statistical models usually assume measurement has taken place, but much stands to be gained from a clear distinction between inter- and intra-variable models. And so I respectfully disagree with those who assert that “the Rasch model is first of all a statistical model.” Maxwell’s method of making analogies from well known physical laws (Nersessian, 2002; Turner, 1955) was adopted by Rasch (1960, pp. 110-115) so that his model would have the same structure as the laws of physics.

Statistical models are a different class of models from the laws of physics (Meehl, 1967), since they allow cross-variable interactions in ways that compromise and defeat the possibility of testing the hypotheses of constant unit size, parameter separation, sufficiency, etc.

I’d like to suggest a paraphrase of the first sentence of the abstract from a recent paper (Silva, 2007) on using analogies in science education: Despite its great importance, many students and even their teachers still cannot recognize the relevance of measurement models to build up psychosocial knowledge and are unable to develop qualitative explanations for mathematical expressions of the lawful structural invariances that exist within the social sciences.

And so, here’s a challenge: we need to make an analogy from Silva’s (2007) work in physics science education and develop a curriculum for social science education that follows a parallel track. We could trace the development of reading measurement from Rasch (1960) through the Anchor Test Study (Jaeger, 1973; Rentz & Bashaw, 1977) to the introduction of the Lexile Framework for Reading (Stenner, 2001) and its explicit continuity with Rasch’s use of Maxwell’s method of analogy (Burdick, Stone, & Stenner, 2006) and full blown predictive theory (Stenner & Stone, 2003).

With the example of the Rasch Reading Law in hand, we could then train students and teachers to think about structural invariance in the context of psychosocial constructs. It may be that, without the development and dissemination of at least a college-level curriculum of this kind, we will never overcome the confusion between statistical and measurement models.

References

Andersen, E. B. (1995). What George Rasch would have thought about this book. In G. H. Fischer & I. W. Molenaar (Eds.), Rasch models: Foundations, recent developments, and applications (pp. 383-390). New York: Springer-Verlag.

Burdick, D. S., Stone, M. H., & Stenner, A. J. (2006). The Combined Gas Law and a Rasch Reading Law. Rasch Measurement Transactions, 20(2), 1059-60 [http://www.rasch.org/rmt/rmt202.pdf].

Jaeger, R. M. (1973). The national test equating study in reading (The Anchor Test Study). Measurement in Education, 4, 1-8.

Meehl, P. E. (1967). Theory-testing in psychology and physics: A methodological paradox. Philosophy of Science, 34(2), 103-115.

Nersessian, N. J. (2002). Maxwell and “the Method of Physical Analogy”: Model-based reasoning, generic abstraction, and conceptual change. In D. Malament (Ed.), Essays in the history and philosophy of science and mathematics (pp. 129-166). Lasalle, Illinois: Open Court.

Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests (Reprint, with Foreword and Afterword by B. D. Wright, Chicago: University of Chicago Press, 1980). Copenhagen, Denmark: Danmarks Paedogogiske Institut.

Rasch, G. (1961). On general laws and the meaning of measurement in psychology. In Proceedings of the fourth Berkeley symposium on mathematical statistics and probability (pp. 321-333 [http://www.rasch.org/memo1960.pdf]). Berkeley, California: University of California Press.

Rentz, R. R., & Bashaw, W. L. (1977, Summer). The National Reference Scale for Reading: An application of the Rasch model. Journal of Educational Measurement, 14(2), 161-179.

Silva, C. C. (2007, August). The role of models and analogies in the electromagnetic theory: A historical case study. Science & Education, 16(7-8), 835-848.

Stenner, A. J. (2001). The Lexile Framework: A common metric for matching readers and texts. California School Library Journal, 25(1), 41-2.

Stenner, A. J., & Stone, M. (2003). Item specification vs. item banking. Rasch Measurement Transactions, 17(3), 929-30 [http://www.rasch.org/rmt/rmt173a.htm].

Turner, J. (1955, November). Maxwell on the method of physical analogy. British Journal for the Philosophy of Science, 6, 226-238.

LivingCapitalMetrics Blog by William P. Fisher, Jr., Ph.D. is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License.
Based on a work at livingcapitalmetrics.wordpress.com.
Permissions beyond the scope of this license may be available at http://www.livingcapitalmetrics.com.

Statistics and Measurement: Clarifying the Differences

Measurement is qualitatively and paradigmatically quite different from statistics, even though statistics obviously play important roles in measurement, and vice versa. The perception of measurement as conceptually difficult stems in part from its rearrangement of most of the concepts that we take for granted in the statistical paradigm as landmarks of quantitative thinking. When we recognize and accept the qualitative differences between statistics and measurement, they both become easier to understand.

Statistical analyses are commonly referred to as quantitative, even though the numbers analyzed most usually have not been derived from the mapping of an invariant substantive unit onto a number line. Measurement takes such mapping as its primary concern, focusing on the quantitative meaningfulness of numbers (Falmagne & Narens, 1983; Luce, 1978; ,  Marcus-Roberts & Roberts, 1987; Mundy, 1986; Narens, 2002; Roberts, 1999). Statistical models focus on group processes and relations among variables, while measurement models focus on individual processes and relations within variables (Duncan, 1992; Duncan & Stenbeck, 1988; Rogosa, 1987). Statistics makes assumptions about factors beyond its control, while measurement sets requirements for objective inference (Andrich, 1989). Statistics primarily involves data analysis, while measurement primarily calibrates instruments in common metrics for interpretation at the point of use (Cohen, 1994; Fisher, 2000; Guttman, 1985; Goodman, 1999a-c; Rasch, 1960).

Statistics focuses on making the most of the data in hand, while measurement focuses on using the data in hand to inform (a) instrument calibration and improvement, and (b) the prediction and efficient gathering of meaningful new data on individuals in practical applications. Where statistical “measures” are defined inherently by a particular analytic method, measures read from calibrated instruments—and the raw observations informing these measures—need not be computerized for further analysis.

Because statistical “measures” are usually derived from ordinal raw scores, changes to the instrument change their meaning, resulting in a strong inclination to avoid improving the instrument. Measures, in contrast, take missing data into account, so their meaning remains invariant over instrument configurations, resulting in a firm basis for the emergence of a measurement quality improvement culture. So statistical “measurement” begins and ends with data analysis, where measurement from calibrated instruments is in a constant cycle of application, new item calibrations, and critical recalibrations that require only intermittent resampling.

The vast majority of statistical methods and models make strong assumptions about the nature of the unit of measurement, but provide either very limited ways of checking those assumptions, or no checks at all. Statistical models are descriptive in nature, meaning that models are fit to data, that the validity of the data is beyond the immediate scope of interest, and that the model accounting for the most variation is regarded as best. Finally, and perhaps most importantly, statistical models are inherently oriented toward the relations among variables at the level of samples and populations.

Measurement models, however, impose strong requirements on data quality in order to achieve the unit of measurement that is easiest to think with, one that stays constant and remains invariant across the local particulars of instrument and sample. Measurement methods and models, then, provide extensive and varied ways of checking the quality of the unit, and so must be prescriptive rather than descriptive. That is, measurement models define the data quality that must be obtained for objective inference. In the measurement paradigm, data are fit to models, data quality is of paramount interest, and data quality evaluation must be informed as much by qualitative criteria as by quantitative.

To repeat the most fundamental point, measurement models are oriented toward individual-level response processes, not group-level aggregate processes. Herbert Blumer pointed out as early as 1930 that quantitative method is not equivalent to statistical method, and that the natural sciences had conspicuous degrees of success long before the emergence of statistical techniques (Hammersly, 1989, pp. 113-4). Both the initial scientific revolution in the 16th-17th centuries and the second scientific revolution of the 19th century found a basis in measurement for publicly objective and reproducible results, but statistics played little or no role in the major discoveries of the times.

The scientific value of statistics resides largely in the reproducibility of cross-variable data relations, and statisticians widely agree that statistical analyses should depend only on sufficient statistics (Arnold, 1982, p. 79). Measurement theoreticians and practitioners also agree, but the sufficiency of the mean and standard deviation relative to a normal distribution is one thing, and the sufficiency of individual responses relative to an invariant construct is quite another (Andersen, 1977; Arnold, 1985; Dynkin, 1951; Fischer, 1981; Hall, Wijsman, & Ghosh, 1965; van der Linden, 1992).

It is of historical interest, though, to point out that Rasch, foremost proponent of the latter, attributes credit for the general value of the concept of sufficiency to Ronald Fisher, foremost proponent of the former. Rasch’s strong statements concerning the fundamental inferential value of sufficiency (Andrich, 1997; Rasch, 1977; Wright, 1980) would seem to contradict his repeated joke about burning all the statistics texts making use of the normal distribution (Andersen, 1995, p. 385) were it not for the paradigmatic distinction between statistical models of group-level relations among variables, and measurement models of individual processes. Indeed, this distinction is made on the first page of Rasch’s (1980) book.

Now we are in a position to appreciate a comment by Ernst Rutherford, the winner of the 1908 Nobel Prize in Chemistry, who held that, if you need statistics to understand the results of your experiment, then you should have designed a better experiment (Wise, 1995, p. 11). A similar point was made by Feinstein (1995) concerning meta-analysis. The rarely appreciated point is that the generalizable replication and application of results depends heavily on the existence of a portable and universally uniform observational framework. The inferences, judgments, and adjustments that can be made at the point of use by clinicians, teachers, managers, etc. provided with additive measures expressed in a substantively meaningful common metric far outstrip those that can be made using ordinal measures expressed in instrument- and sample-dependent scores. See Andrich (1989, 2002, 2004), Cohen (1994), Davidoff (1999), Duncan (1992), Embretson (1996), Goodman (1999a, 1999b, 1999c), Guttman (1981, 1985), Meehl (1967), Michell (1986), Rogosa (1987), Romanowski and Douglas (2002), and others for more on this distinction between statistics and measurement.

These contrasts show that the confounding of statistics and measurement is a problem of vast significance that persists in spite of repeated efforts to clarify the distinction. For a wide variety of reasons ranging from cultural presuppositions about the nature of number to the popular notion that quantification is as easy as assigning numbers to observations, measurement is not generally well understood by the public (or even by statisticians!). And so statistics textbooks rarely, if ever, include even passing mention of instrument calibration methods, metric equating processes, the evaluation of data quality relative to the requirements of objective inference, traceability to metrological reference standards, or the integration of qualitative and quantitative methods in the interpretation of measures.

Similarly, in business, marketing, health care, and quality improvement circles, we find near-universal repetition of the mantra, “You manage what you measure,” with very little or no attention paid to the quality of the numbers treated as measures. And so, we find ourselves stuck with so-called measurement systems where,

• instead of linear measures defined by a unit that remains constant across samples and instruments we saddle ourselves with nonlinear scores and percentages defined by units that vary in unknown ways across samples and instruments;
• instead of availing ourselves of the capacity to take missing data into account, we hobble ourselves with the need for complete data;
• instead of dramatically reducing data volume with no loss of information, we insist on constantly re-enacting the meaningless ritual of poring over undigestible masses of numbers;
• instead of adjusting measures for the severity or leniency of judges assigning ratings, we allow measures to depend unfairly on which rater happens to make the observations;
• instead of using methods that give the same result across different distributions, we restrict ourselves to ones that give different results when assumptions of normality are not met and/or standard deviations differ;
• instead of calibrating instruments in an experimental test of the hypothesis that the intended construct is in fact structured in such a way as to make its mapping onto a number line meaningful, we assign numbers and make quantitative inferences with no idea as to whether they relate at all to anything real;
• instead of checking to see whether rating scales work as intended, with higher ratings consistently representing more of the variable, we make assumptions that may be contradicted by the order and spacing of the way rating scales actually work in practice;
• instead of defining a comprehensive framework for interpreting measures relative to a construct, we accept the narrow limits of frameworks defined by the local sample and items;
• instead of capitalizing on the practicality and convenience of theories capable of accurately predicting item calibrations and measures apart from data, we counterproductively define measurement empirically in terms of data analysis;
• instead of putting calibrated tools into the hands of front-line managers, service representatives, teachers and clinicians, we require them to submit to cumbersome data entry, analysis, and reporting processes that defeat the purpose of measurement by ensuring the information provided is obsolete by the time it gets back to the person who could act on it; and
• instead of setting up efficient systems for communicating meaningful measures in common languages with shared points of reference, we settle for inefficient systems for communicating meaningless scores in local incommensurable languages.

Because measurement is simultaneously ubiquitous and rarely well understood, we find ourselves in a world that gives near-constant lip service to the importance of measurement while it does almost nothing to provide measures that behave the way we assume they do. This state of affairs seems to have emerged in large part due to our failure to distinguish between the group-level orientation of statistics and the individual-level orientation of measurement. We seem to have been seduced by a variation on what Whitehead (1925, pp. 52-8) called the fallacy of misplaced concreteness. That is, we have assumed that the power of lawful regularities in thought and behavior would be best revealed and acted on via statistical analyses of data that themselves embody the aggregate mass of the patterns involved.

It now appears, however, in light of studies in the history of science (Latour, 1987, 2005; Wise, 1995), that an alternative and likely more successful approach will be to capitalize on the “wisdom of crowds” (Surowiecki, 2004) phenomenon of collective, distributed cognition (Akkerman, et al., 2007; Douglas, 1986; Hutchins, 1995; Magnus, 2007). This will be done by embodying lawful regularities in instruments calibrated in ideal, abstract, and portable metrics put to work by front-line actors on mass scales (Fisher, 2000, 2005, 2009a, 2009b). In this way, we will inform individual decision processes and structure communicative transactions with efficiencies, meaningfulness, substantive effectiveness, and power that go far beyond anything that could be accomplished by trying to make inferences about individuals from group-level statistics.

We ought not accept the factuality of data as the sole criterion of objectivity, with all theory and instruments constrained by and focused on the passing ephemera of individual sets of local particularities. Properly defined and operationalized via a balanced interrelation of theory, data, and instrument, advanced measurement is not a mere mathematical exercise but offers a wealth of advantages and conveniences that cannot otherwise be obtained. We ignore its potentials at our peril.

References
Akkerman, S., Van den Bossche, P., Admiraal, W., Gijselaers, W., Segers, M., Simons, R.-J., et al. (2007, February). Reconsidering group cognition: From conceptual confusion to a boundary area between cognitive and socio-cultural perspectives? Educational Research Review, 2, 39-63.

Andersen, E. B. (1977). Sufficient statistics and latent trait models. Psychometrika, 42(1), 69-81.

Andersen, E. B. (1995). What George Rasch would have thought about this book. In G. H. Fischer & I. W. Molenaar (Eds.), Rasch models: Foundations, recent developments, and applications (pp. 383-390). New York: Springer-Verlag.

Andrich, D. (1989). Distinctions between assumptions and requirements in measurement in the social sciences. In J. A. Keats, R. Taft, R. A. Heath & S. H. Lovibond (Eds.), Mathematical and Theoretical Systems: Proceedings of the 24th International Congress of Psychology of the International Union of Psychological Science, Vol. 4 (pp. 7-16). North-Holland: Elsevier Science Publishers.

Andrich, D. (1997). Georg Rasch in his own words [excerpt from a 1979 interview]. Rasch Measurement Transactions, 11(1), 542-3. [http://www.rasch.org/rmt/rmt111.htm#Georg].

Andrich, D. (2002). Understanding resistance to the data-model relationship in Rasch’s paradigm: A reflection for the next generation. Journal of Applied Measurement, 3(3), 325-59.

Andrich, D. (2004, January). Controversy and the Rasch model: A characteristic of incompatible paradigms? Medical Care, 42(1), I-7–I-16.

Arnold, S. F. (1982-1988). Sufficient statistics. In S. Kotz, N. L. Johnson & C. B. Read (Eds.), Encyclopedia of Statistical Sciences (pp. 72-80). New York: John Wiley & Sons.

Arnold, S. F. (1985, September). Sufficiency and invariance. Statistics & Probability Letters, 3, 275-279.

Cohen, J. (1994). The earth is round (p < 0.05). American Psychologist, 49, 997-1003.

Davidoff, F. (1999, 15 June). Standing statistics right side up (Editorial). Annals of Internal Medicine, 130(12), 1019-1021.

Douglas, M. (1986). How institutions think. Syracuse, New York: Syracuse University Press.

Dynkin, E. B. (1951). Necessary and sufficient statistics for a family of probability distributions. Selected Translations in Mathematical Statistics and Probability, 1, 23-41.

Duncan, O. D. (1992, September). What if? Contemporary Sociology, 21(5), 667-668.

Duncan, O. D., & Stenbeck, M. (1988). Panels and cohorts: Design and model in the study of voting turnout. In C. C. Clogg (Ed.), Sociological Methodology 1988 (pp. 1-35). Washington, DC: American Sociological Association.

Embretson, S. E. (1996, September). Item Response Theory models and spurious interaction effects in factorial ANOVA designs. Applied Psychological Measurement, 20(3), 201-212.

Falmagne, J.-C., & Narens, L. (1983). Scales and meaningfulness of quantitative laws. Synthese, 55, 287-325.

Feinstein, A. R. (1995, January). Meta-analysis: Statistical alchemy for the 21st century. Journal of Clinical Epidemiology, 48(1), 71-79.

Fischer, G. H. (1981, March). On the existence and uniqueness of maximum-likelihood estimates in the Rasch model. Psychometrika, 46(1), 59-77.

Fisher, W. P., Jr. (2000). Objectivity in psychosocial measurement: What, why, how. Journal of Outcome Measurement, 4(2), 527-563.

Fisher, W. P., Jr. (2005). Daredevil barnstorming to the tipping point: New aspirations for the human sciences. Journal of Applied Measurement, 6(3), 173-9.

Fisher, W. P., Jr. (2009a). Bringing human, social, and natural capital to life: Practical consequences and opportunities. In M. Wilson, K. Draney, N. Brown & B. Duckor (Eds.), Advances in Rasch Measurement, Vol. Two (p. in press). Maple Grove, MN: JAM Press.

Fisher, W. P., Jr. (2009b, July). Invariance and traceability for measures of human, social, and natural capital: Theory and application. Measurement (Elsevier), in press.

Goodman, S. N. (1999a, 6 April). Probability at the bedside: The knowing of chances or the chances of knowing? (Editorial). Annals of Internal Medicine, 130(7), 604-6.

Goodman, S. N. (1999b, 15 June). Toward evidence-based medical statistics. 1: The p-value fallacy. Annals of Internal Medicine, 130(12), 995-1004.

Goodman, S. N. (1999c, 15 June). Toward evidence-based medical statistics. 2: The Bayes factor. Annals of Internal Medicine, 130(12), 1005-1013.

Guttman, L. (1981). What is not what in theory construction. In I. Borg (Ed.), Multidimensional data representations: When & why. Ann Arbor, MI: Mathesis Press.

Guttman, L. (1985). The illogic of statistical inference for cumulative science. Applied Stochastic Models and Data Analysis, 1, 3-10.

Hall, W. J., Wijsman, R. A., & Ghosh, J. K. (1965). The relationship between sufficiency and invariance with applications in sequential analysis. Annals of Mathematical Statistics, 36, 575-614.

Hammersley, M. (1989). The dilemma of qualitative method: Herbert Blumer and the Chicago Tradition. New York: Routledge.

Hutchins, E. (1995). Cognition in the wild. Cambridge, Massachusetts: MIT Press.

Latour, B. (1987). Science in action: How to follow scientists and engineers through society. New York: Cambridge University Press.

Latour, B. (1995). Cogito ergo sumus! Or psychology swept inside out by the fresh air of the upper deck: Review of Hutchins’ Cognition in the Wild, MIT Press, 1995. Mind, Culture, and Activity: An International Journal, 3(192), 54-63.

Latour, B. (2005). Reassembling the social: An introduction to Actor-Network-Theory. (Clarendon Lectures in Management Studies). Oxford, England: Oxford University Press.

Luce, R. D. (1978, March). Dimensionally invariant numerical laws correspond to meaningful qualitative relations. Philosophy of Science, 45, 1-16.

Magnus, P. D. (2007). Distributed cognition and the task of science. Social Studies of Science, 37(2), 297-310.

Marcus-Roberts, H., & Roberts, F. S. (1987). Meaningless statistics. Journal of Educational Statistics, 12(4), 383-394.

Meehl, P. E. (1967). Theory-testing in psychology and physics: A methodological paradox. Philosophy of Science, 34(2), 103-115.

Michell, J. (1986). Measurement scales and statistics: A clash of paradigms. Psychological Bulletin, 100, 398-407.

Mundy, B. (1986, June). On the general theory of meaningful representation. Synthese, 67(3), 391-437.

Narens, L. (2002, December). A meaningful justification for the representational theory of measurement. Journal of Mathematical Psychology, 46(6), 746-68.

Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests (Reprint, with Foreword and Afterword by B. D. Wright, Chicago: University of Chicago Press, 1980). Copenhagen, Denmark: Danmarks Paedogogiske Institut.

Rasch, G. (1977). On specific objectivity: An attempt at formalizing the request for generality and validity of scientific statements. Danish Yearbook of Philosophy, 14, 58-94.

Roberts, F. S. (1999). Meaningless statements. In R. Graham, J. Kratochvil, J. Nesetril & F. Roberts (Eds.), Contemporary trends in discrete mathematics, DIMACS Series, Volume 49 (pp. 257-274). Providence, RI: American Mathematical Society.

Rogosa, D. (1987). Casual [sic] models do not support scientific conclusions: A comment in support of Freedman. Journal of Educational Statistics, 12(2), 185-95.

Romanoski, J. T., & Douglas, G. (2002). Rasch-transformed raw scores and two-way ANOVA: A simulation analysis. Journal of Applied Measurement, 3(4), 421-430.

Stevens, S. S. (1951). Mathematics, measurement, and psychophysics. In S. S. Stevens (Ed.), Handbook of experimental psychology (pp. 1-49). New York: John Wiley & Sons.

Surowiecki, J. (2004). The wisdom of crowds: Why the many are smarter than the few and how collective wisdom shapes business, economies, societies and nations. New York: Doubleday.

van der Linden, W. J. (1992). Sufficient and necessary statistics. Rasch Measurement Transactions, 6(3), 231 [http://www.rasch.org/rmt/rmt63d.htm].

Whitehead, A. N. (1925). Science and the modern world. New York: Macmillan.

Wise, M. N. (Ed.). (1995). The values of precision. Princeton, New Jersey: Princeton University Press.

Wright, B. D. (1980). Foreword, Afterword. In Probabilistic models for some intelligence and attainment tests, by Georg Rasch (pp. ix-xix, 185-199. http://www.rasch.org/memo63.htm) [Reprint; original work published in 1960 by the Danish Institute for Educational Research]. Chicago, Illinois: University of Chicago Press.

LivingCapitalMetrics Blog by William P. Fisher, Jr., Ph.D. is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License.
Based on a work at livingcapitalmetrics.wordpress.com.
Permissions beyond the scope of this license may be available at http://www.livingcapitalmetrics.com.

Contesting the Claim, Part III: References

References

Andersen, E. B. (1977). Sufficient statistics and latent trait models. Psychometrika, 42(1), 69-81.

Andersen, E. B. (1995). What George Rasch would have thought about this book. In G. H. Fischer & I. W. Molenaar (Eds.), Rasch models: Foundations, recent developments, and applications (pp. 383-390). New York: Springer-Verlag.

Andrich, D. (1988). Rasch models for measurement. (Vols. series no. 07-068). Sage University Paper Series on Quantitative Applications in the Social Sciences). Beverly Hills, California: Sage Publications.

Andrich, D. (1998). Thresholds, steps and rating scale conceptualization. Rasch Measurement Transactions, 12(3), 648-9 [http://209.238.26.90/rmt/rmt1239.htm].

Arnold, S. F. (1985, September). Sufficiency and invariance. Statistics & Probability Letters, 3, 275-279.

Bond, T., & Fox, C. (2001). Applying the Rasch model: Fundamental measurement in the human sciences. Mahwah, New Jersey: Lawrence Erlbaum Associates.

Burdick, D. S., Stone, M. H., & Stenner, A. J. (2006). The Combined Gas Law and a Rasch Reading Law. Rasch Measurement Transactions, 20(2), 1059-60 [http://www.rasch.org/rmt/rmt202.pdf].

Burdick, H., & Stenner, A. J. (1996). Theoretical prediction of test items. Rasch Measurement Transactions, 10(1), 475 [http://www.rasch.org/rmt/rmt101b.htm].

Choi, E. (1998, Spring). Rasch invents “Ounces.” Popular Measurement, 1(1), 29 [http://www.rasch.org/pm/pm1-29.pdf].

Cohen, J. (1994). The earth is round (p < 0.05). American Psychologist, 49, 997-1003.

DeBoeck, P., & Wilson, M. (Eds.). (2004). Explanatory item response models: A generalized linear and nonlinear approach. (Statistics for Social and Behavioral Sciences). New York: Springer-Verlag.

Dynkin, E. B. (1951). Necessary and sufficient statistics for a family of probability distributions. Selected Translations in Mathematical Statistics and Probability, 1, 23-41.

Embretson, S. E. (1996, September). Item Response Theory models and spurious interaction effects in factorial ANOVA designs. Applied Psychological Measurement, pp. 201-212.

Falmagne, J.-C., & Narens, L. (1983). Scales and meaningfulness of quantitative laws. Synthese, 55, 287-325.

Fischer, G. H. (1981, March). On the existence and uniqueness of maximum-likelihood estimates in the Rasch model. Psychometrika, 46(1), 59-77.

Fischer, G. H. (1995). Derivations of the Rasch model. In G. Fischer & I. Molenaar (Eds.), Rasch models: Foundations, recent developments, and applications (pp. 15-38). New York: Springer-Verlag.

Fisher, W. P., Jr. (1988). Truth, method, and measurement: The hermeneutic of instrumentation and the Rasch model [diss]. Dissertation Abstracts International, 49, 0778A, Dept. of Education, Division of the Social Sciences: University of Chicago (376 pages, 23 figures, 31 tables).

Fisher, W. P., Jr. (1997). Physical disability construct convergence across instruments: Towards a universal metric. Journal of Outcome Measurement, 1(2), 87-113.

Fisher, W. P., Jr. (1997, June). What scale-free measurement means to health outcomes research. Physical Medicine & Rehabilitation State of the Art Reviews, 11(2), 357-373.

Fisher, W. P., Jr. (1999). Foundations for health status metrology: The stability of MOS SF-36 PF-10 calibrations across samples. Journal of the Louisiana State Medical Society, 151(11), 566-578.

Fisher, W. P., Jr. (2000). Objectivity in psychosocial measurement: What, why, how. Journal of Outcome Measurement, 4(2), 527-563.

Fisher, W. P., Jr. (2004, October). Meaning and method in the social sciences. Human Studies: A Journal for Philosophy and the Social Sciences, 27(4), 429-54.

Fisher, W. P., Jr. (2008, Summer). The cash value of reliability. Rasch Measurement Transactions, 22(1), 1160-3 [http://www.rasch.org/rmt/rmt221.pdf].

Fisher, W. P., Jr. (2009, July). Invariance and traceability for measures of human, social, and natural capital: Theory and application. Measurement (Elsevier), in press.

Goodman, S. N. (1999, 15 June). Toward evidence-based medical statistics. 1: The p-value fallacy. Annals of Internal Medicine, 130(12), 995-1004.

Guttman, L. (1985). The illogic of statistical inference for cumulative science. Applied Stochastic Models and Data Analysis, 1, 3-10.

Hall, W. J., Wijsman, R. A., & Ghosh, J. K. (1965). The relationship between sufficiency and invariance with applications in sequential analysis. Annals of Mathematical Statistics, 36, 575-614.

Linacre, J. M. (1993). Rasch-based generalizability theory. Rasch Measurement Transactions, 7(1), 283-284 [http://www.rasch.org/rmt/rmt71h.htm].

Luce, R. D., & Tukey, J. W. (1964). Simultaneous conjoint measurement: A new kind of fundamental measurement. Journal of Mathematical Psychology, 1(1), 1-27.

Meehl, P. E. (1967). Theory-testing in psychology and physics: A methodological paradox. Philosophy of Science, 34(2), 103-115.

Meehl, P. E. (1978). Theoretical risks and tabular asterisks: Sir Karl, Sir Ronald, and the slow progress of soft psychology. Journal of Consulting and Clinical Psychology, 46, 806-34.

Michell, J. (1999). Measurement in psychology: A critical history of a methodological concept. Cambridge: Cambridge University Press.

Moulton, M. (1993). Probabilistic mapping. Rasch Measurement Transactions, 7(1), 268 [http://www.rasch.org/rmt/rmt71b.htm].

Mundy, B. (1986, June). On the general theory of meaningful representation. Synthese, 67(3), 391-437.

Narens, L. (2002). Theories of meaningfulness (S. W. Link & J. T. Townsend, Eds.). Scientific Psychology Series. Mahwah, New Jersey: Lawrence Erlbaum Associates.

Newby, V. A., Conner, G. R., Grant, C. P., & Bunderson, C. V. (2009). The Rasch model and additive conjoint measurement. Journal of Applied Measurement, 10(4), 348-354.

Pelton, T., & Bunderson, V. (2003). The recovery of the density scale using a stochastic quasi-realization of additive conjoint measurement. Journal of Applied Measurement, 4(3), 269-81.

Ramsay, J. O., Bloxom, B., & Cramer, E. M. (1975, June). Review of Foundations of Measurement, Vol. 1, by D. H. Krantz et al. Psychometrika, 40(2), 257-262.

Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests (Reprint, with Foreword and Afterword by B. D. Wright, Chicago: University of Chicago Press, 1980). Copenhagen, Denmark: Danmarks Paedogogiske Institut.

Roberts, F. S., & Rosenbaum, Z. (1986). Scale type, meaningfulness, and the possible psychophysical laws. Mathematical Social Sciences, 12, 77-95.

Romanoski, J. T., & Douglas, G. (2002). Rasch-transformed raw scores and two-way ANOVA: A simulation analysis. Journal of Applied Measurement, 3(4), 421-430.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological Bulletin, 57(5), 416-428.

Smith, R. M., & Taylor, P. (2004). Equating rehabilitation outcome scales: Developing common metrics. Journal of Applied Measurement, 5(3), 229-42.

Thurstone, L. L. (1928). Attitudes can be measured. American Journal of Sociology, XXXIII, 529-544. Reprinted in L. L. Thurstone, The Measurement of Values. Midway Reprint Series. Chicago, Illinois: University of Chicago Press, 1959, pp. 215-233.

van der Linden, W. J. (1992). Sufficient and necessary statistics. Rasch Measurement Transactions, 6(3), 231 [http://www.rasch.org/rmt/rmt63d.htm].

Velleman, P. F., & Wilkinson, L. (1993). Nominal, ordinal, interval, and ratio typologies are misleading. The American Statistician, 47(1), 65-72.

Wright, B. D. (1977). Solving measurement problems with the Rasch model. Journal of Educational Measurement, 14(2), 97-116 [http://www.rasch.org/memo42.htm].

Wright, B. D. (1997, Winter). A history of social science measurement. Educational Measurement: Issues and Practice, pp. 33-45, 52 [http://www.rasch.org/memo62.htm].

LivingCapitalMetrics Blog by William P. Fisher, Jr., Ph.D. is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License.
Based on a work at livingcapitalmetrics.wordpress.com.
Permissions beyond the scope of this license may be available at http://www.livingcapitalmetrics.com.

Contesting the Claim, Part II: Are Rasch Measures Really as Objective as Physical Measures?

When a raw score is sufficient to the task of measurement, the model is the Rasch model, we can estimate the parameters consistently, and we can evaluate the fit of the data to the model. The invariance properties that follow from a sufficient statistic include virtually the entire class of invariant rules (Hall, Wijsman, & Ghosh, 1965; Arnold, 1985), and similar relationships with other key measurement properties follow from there (Fischer, 1981, 1995; Newby, Conner, Grant, & Bunderson, 2009; Wright, 1977, 1997).

What does this all actually mean? Imagine we were able to ask an infinite number of people an infinite number of questions that all work together to measure the same thing. Because (1) the scores are sufficient statistics, (2) the ruler is not affected by what is measured, (3) the parameters separate, and (4) the data fit the model, any subset of the questions asked would give the same measure. This means that any subscore for any person measured would be a function of any and all other subscores. When a sufficient statistic is a function of all other sufficient statistics, it is not only sufficient, it is necessary, and is referred to as a minimally sufficient statistic. Thus, if separable, independent model parameters can be estimated, the model must be the Rasch model, and the raw score is both sufficient and necessary (Andersen, 1977; Dynkin, 1951; van der Linden, 1992).

This means that scores, ratings, and percentages actually stand for something measurable only when they fit a Rasch model.  After all, what actually would be the point of using data that do not support the estimation of independent parameters? If the meaning of the results is tied in unknown ways to the specific particulars of a given situation, then those results are meaningless, by definition (Roberts & Rosenbaum, 1986; Falmagne & Narens, 1983; Mundy, 1986; Narens, 2002; also see Embretson, 1996; Romanoski and Douglas, 2002). There would be no point in trying to learn anything from them, as whatever happened was a one-time unique event that tells us nothing we can use in any future event (Wright, 1977, 1997).

What we’ve done here is akin to taking a narrative stroll through a garden of mathematical proofs. These conceptual analyses can be very convincing, but actual demonstrations of them are essential. Demonstrations would be especially persuasive if there would be some way of showing three things. First, shouldn’t there be some way of constructing ordinal ratings or scores for one or another physical variable that, when scaled, give us measures that are the same as the usual measures we are accustomed to?

This would show that we can use the type of instrument usually found in the social sciences to construct physical measures with the characteristics we expect. There are four available examples, in fact, involving paired comparisons of weights (Choi, 1998), measures of short lengths (Fisher, 1988), ratings of medium-range distances (Moulton, 1993), and a recovery of the density scale (Pelton & Bunderson, 2003). In each case, the Rasch-calibrated experimental instruments produced measures equivalent to the controls, as shown in linear plots of the pairs of measures.

A second thing to build out from the mathematical proofs are experiments in which we check the purported stability of measures and calibrations. We can do this by splitting large data sets, using different groups of items to produce two or more measures for each person, or using different groups of respondents/examinees to provide data for two or more sets of item calibrations. This is a routine experimental procedure in many psychometric labs, and results tend to conform with theory, with strong associations found between increasing sample sizes and increasing reliability coefficients for the respective measures or calibrations. These associations can be plotted (Fisher, 2008), as can the pairs of calibrations estimated from different samples (Fisher, 1999), and the pairs of measures estimated from different instruments (Fisher, Harvey, Kilgore, et al., 1995; Smith & Taylor, 2004). The theoretical expectation of tighter plots for better designed instruments, larger sample sizes, and longer tests is confirmed so regularly that it should itself have the status of a law of nature (Linacre, 1993).

A third convincing demonstration is to compare studies of the same thing conducted in different times and places by different researchers using different instruments on different samples. If the instruments really measure the same thing, there will not only be obvious similarities in their item contents, but similar items will calibrate in similar positions on the metric across samples. Results of this kind have been obtained in at least three published studies (Fisher, 1997a, 1997b; Belyukova, Stone, & Fox, 2004).

All of these arguments are spelled out in greater length and detail, with illustrations, in a forthcoming article (Fisher, 2009). I learned all of this from Benjamin Wright, who worked directly with Rasch himself, and who, perhaps more importantly, was prepared for what he could learn from Rasch in his previous career as a physicist. Before encountering Rasch in 1960, Wright had worked with Feynman at Cornell, Townes at Bell Labs, and Mulliken at the University of Chicago. Taught and influenced not just by three of the great minds of twentieth-century physics, but also by Townes’ philosophical perspectives on meaning and beauty, Wright had left physics in search of life. He was happy to transfer his experience with computers into his new field of educational research, but he was dissatisfied with the quality of the data and how it was treated.

Rasch’s ideas gave Wright the conceptual tools he needed to integrate his scientific values with the demands of the field he was in. Over the course of his 40-year career in measurement, Wright wrote the first software for estimating Rasch model parameters and continuously improved it; he adapted new estimation algorithms for Rasch’s models and was involved in the articulation of new models; he applied the models to hundreds of data sets using his software; he vigorously invested himself in students and colleagues; he founded new professional societies, meetings, and journals;  and he never stopped learning how to think anew about measurement and the meaning of numbers. Through it all, there was always a yardstick handy as a simple way of conveying the basic requirements of measurement as we intuitively understand it in physical terms.

Those of us who spend a lot of time working with these ideas and trying them out on lots of different kinds of data forget or never realize how skewed our experience is relative to everyone else’s. I guess a person lives in a different world when you have the sustained luxury of working with very large databases, as I have had, and you see the constancy and stability of well-designed measures and calibrations over time, across instruments, and over repeated samples ranging from 30 to several million.

When you have that experience, it becomes a basic description of reasonable expectation to read the work of a colleague and see him say that “when the key features of a statistical model relevant to the analysis of social science data are the same as those of the laws of physics, then those features are difficult to ignore” (Andrich, 1988, p. 22). After calibrating dozens of instruments over 25 years, some of them many times over, it just seems like the plainest statement of the obvious to see the same guy say “Our measurement principles should be the same for properties of rocks as for the properties of people. What we say has to be consistent with physical measurement” (Andrich, 1998, p. 3).

And I find myself wishing more people held the opinion expressed by two other colleagues, that “scientific measures in the social sciences must hold to the same standards as do measures in the physical sciences if they are going to lead to the same quality of generalizations” (Bond & Fox, 2001, p. 2). When these sentiments are taken to their logical conclusion in a practical application, the real value of “attempting for reading comprehension what Newtonian mechanics achieved for astronomy” (Burdick & Stenner, 1996) becomes apparent. Rasch’s analogy of the structure of his model for reading tests and Newton’s Second Law can be restated relative to any physical law expressed as universal conditionals among variable triplets; a theory of the variable measured capable of predicting item calibrations provides the causal story for the observed variation (Burdick, Stone, & Stenner, 2006; DeBoeck & Wilson, 2004).

Knowing what I know, from the mathematical principles I’ve been trained in and from the extensive experimental work I’ve done, it seems amazing that so little attention is actually paid to tools and concepts that receive daily lip service as to their central importance in every facet of life, from health care to education to economics to business. Measurement technology rose up decades ago in preparation for the demands of today’s challenges. It is just plain weird the way we’re not using it to anything anywhere near its potential.

I’m convinced, though, that the problem is not a matter of persuasive rhetoric applied to the minds of the right people. Rather, someone, hopefully me, has got to configure the right combination of players in the right situation at the right time and at the right place to create a new form of real value that can’t be created any other way. Like they say, money talks. Persuasion is all well and good, but things will really take off only when people see that better measurement can aid in removing inefficiencies from the management of human, social, and natural capital, that better measurement is essential to creating sustainable and socially responsible policies and practices, and that better measurement means new sources of profitability.  I’m convinced that advanced measurement techniques are really nothing more than a new form of IT or communications technology. They will fit right into the existing networks and multiply their efficiencies many times over.

And when they do, we may be in a position to finally

“confront the remarkable fact that throughout the gigantic range of physical knowledge numerical laws assume a remarkably simple form provided fundamental measurement has taken place. Although the authors cannot explain this fact to their own satisfaction, the extension to behavioral science is obvious: we may have to await fundamental measurement before we will see any real progress in quantitative laws of behavior. In short, ordinal scales (even continuous ordinal scales) are perhaps not good enough and it may not be possible to live forever with a dozen different procedures for quantifying the same piece of behavior, each making strong but untestable and basically unlikely assumptions which result in nonlinear plots of one scale against another. Progress in physics would have been impossibly difficult without fundamental measurement and the reader who believes that all that is at stake in the axiomatic treatment of measurement is a possible criterion for canonizing one scaling procedure at the expense of others is missing the point” (Ramsay, Bloxom, and Cramer, 1975, p. 262).

LivingCapitalMetrics Blog by William P. Fisher, Jr., Ph.D. is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License.
Based on a work at livingcapitalmetrics.wordpress.com.
Permissions beyond the scope of this license may be available at http://www.livingcapitalmetrics.com.

Contesting the Claim, Part I: Are Rasch Measures Really as Objective as Physical Measures?

Psychometricians, statisticians, metrologists, and measurement theoreticians tend to be pretty unassuming kinds of people. They’re unobtrusive and retiring, by and large. But there is one thing some of them are prone to say that will raise the ire of others in a flash, and the poor innocent geek will suddenly be subjected to previously unknown forms and degrees of social exclusion.

What is that one thing? “Instruments calibrated by fitting data to a Rasch model measure with the same kind of objectivity as is obtained with physical measures.” That’s one version. Another could be along these lines: “When data fit a Rasch model, we’ve discovered a pattern in human attitudes or behaviors so regular that it is conceptually equivalent to a law of nature.”

Maybe it is the implication of objectivity as something that must be politically incorrect that causes the looks of horror and recoiling retreats in the nonmetrically inclined when they hear things like this. Maybe it is the ingrained cultural predisposition to thinking such claims outrageously preposterous that makes those unfamiliar with 80 years of developments and applications so dismissive. Maybe it’s just fear of the unknown, or a desire not to have to be responsible for knowing something important that hardly anyone else knows.

Of course, it could just be a simple misunderstanding. When people hear the word “objective” do most of them have an image of an object in mind? Does objectivity connote physical concreteness to most people? That doesn’t hold up well for me, since we can be objective about events and things people do without any confusions involving being able to touch and feel what’s at issue.

No, I think something else is going on. I think it has to do with the persistent idea that objectivity requires a disconnected, alienated point of view, one that ignores the mutual implication of subject and object in favor of analytically tractable formulations of problems that, though solvable, are irrelevant to anything important or real. But that is hardly the only available meaning of objectivity, and it isn’t anywhere near the best. It certainly is not what is meant in the world of measurement theory and practice.

It’s better to think of objectivity as something having to do with things like the object of a conversation, or an object of linguistic reference: “chair” as referring to the entire class of all forms of seating technology, for instance. In these cases, we know right away that we’re dealing with what might be considered a heuristic ideal, an abstraction. It also helps to think of objectivity in terms of fairness and justice. After all, don’t we want our educational, health care, and social services systems to respect the equality of all individuals and their rights?

That is not, of course, how measurement theoreticians in psychology have always thought about objectivity. In fact, it was only 70-80 years ago that most psychologists gave up on objective measurement because they couldn’t find enough evidence of concrete phenomena to support the claims to objectivity they wanted to make (Michell, 1999). The focus on the reflex arc led a lot of psychologists into psychophysics, and the effects of operant conditioning led others to behaviorism. But a lot of the problems studied in these fields, though solvable, turned out to be uninteresting and unrelated to the larger issues of life demanding attention.

And so, with no physical entity that could be laid end-to-end and concatenated in the way weights are in a balance scale, psychologists just redefined measurement to suit what they perceived to be the inherent limits of their subject matter. Measurement didn’t have to be just ratio or interval, it could also be ordinal and even nominal. The important thing was to get numbers that could be statistically manipulated. That would provide more than enough credibility, or obfuscation, to create the appearance of legitimate science.

But while mainstream psychology was focused on hunting for statistically significant p-values, there were others trying to figure out if attitudes, abilities, and behaviors could be measured in a rigorously meaningful way.

Louis Thurstone, a former electrical engineer turned psychologist, was among the first to formulate the problem. Writing in 1928, Thurstone rightly focused on the instrument as the focus of attention:

“The scale must transcend the group measured.–One crucial experimental test must be applied to our method of measuring attitudes before it can be accepted as valid. A measuring instrument must not be seriously affected in its measuring function by the object of measurement. To the extent that its measuring function is so affected, the validity of the instrument is impaired or limited. If a yardstick measured differently because of the fact that it was a rug, a picture, or a piece of paper that was being measured, then to that extent the trustworthiness of that yardstick as a measuring device would be impaired. Within the range of objects for which the measuring instrument is intended, its function must be independent of the object of measurement”  (Thurstone, 1959, p. 228).

Thurstone aptly captures what is meant when it is said that attitudes, abilities, or behaviors can be measured with the same kind of objectivity as is obtained in the natural sciences. Objectivity is realized when a test, survey, or assessment functions the same way no matter who is being measured, and, conversely (Thurstone took this up, too), an attitude, ability, or behavior exhibits the same amount of what is measured no matter which instrument is used.

This claim, too, may seem to some to be so outrageously improbable as to be worthy of rejecting out of hand. After all, hasn’t everyone learned how the fact of being measured changes the measure? Thing is, this is just as true in physics and ecology as it is in psychiatry or sociology, and the natural sciences haven’t abandoned their claims to objectivity. So what’s up?

What’s up is that all sciences now have participant observers. The old Cartesian duality of the subject-object split still resides in various rhetorical choices and affects our choices and behaviors, but, in actual practice, scientific methods have always had to deal with the way questions imply particular answers.

And there’s more. Qualitative methods have grown out of some of the deep philosophical introspections of the twentieth century, such as phenomenology, hermeneutics, deconstruction, postmodernism, etc. But most researchers who are adopting qualitative methods over quantitative ones don’t know that the philosophers legitimating the new focuses on narrative, interpretation, and the construction of meaning did quite a lot of very good thinking about mathematics and quantitative reasoning. Much of my own published work engages with these philosophers to find new ways of thinking about measurement (Fisher, 2004, for instance). And there are some very interesting connections to be made that show quantification does not necessarily have to involve a positivist, subject-object split.

So where does that leave us? Well, with probability. Not in the sense of statistical hypothesis testing, but in the sense of calibrating instruments with known probabilistic characteristics. If the social sciences are ever to be scientific, null hypothesis significance tests are going to have to be replaced with universally uniform metrics embodying and deploying the regularities of natural laws, as is the case in the physical sciences. Various arguments on this issue have been offered for decades (Cohen, 1994; Meehl, 1967, 1978; Goodman, 1999; Guttman, 1985; Rozeboom, 1960). The point is not to proscribe allowable statistics based on scale type  (Velleman & Wilkinson, 1993). Rather, we need to shift and simplify the focus of inference from the statistical analysis of data to the calibration and distribution of instruments that support distributed cognition, unify networks, lubricate markets, and coordinate collective thinking and acting (Fisher, 2000, 2009). Persuasion will likely matter far less in resolving the matter than an ability to create new value, efficiencies, and profits.

In 1964, Luce and Tukey gave us another way of stating what Thurstone was getting at:

“The axioms of conjoint measurement apply naturally to problems of classical physics and permit the measurement of conventional physical quantities on ratio scales…. In the various fields, including the behavioral and biological sciences, where factors producing orderable effects and responses deserve both more useful and more fundamental measurement, the moral seems clear: when no natural concatenation operation exists, one should try to discover a way to measure factors and responses such that the ‘effects’ of different factors are additive.”

In other words, if we cannot find some physical thing that we can make add up the way numbers do, as we did with length, weight, volts, temperature, time, etc., then we ought to ask questions in a way that allows the answers to reveal the kind of patterns we expect to see when things do concatenate. What Thurstone and others working in his wake have done is to see that we could possibly do some things virtually in terms of abstract relations that we cannot do actually in terms of concrete relations.

The concept is no more difficult to comprehend than understanding the difference between playing solitaire with actual cards and writing a computer program to play solitaire with virtual cards. Either way, the same relationships hold.

A Danish mathematician, Georg Rasch, understood this. Working in the 1950s with data from psychological and reading tests, Rasch worked from his training in the natural sciences and mathematics to arrive at a conception of measurement that would apply in the natural and human sciences equally well. He realized that

“…the acceleration of a body cannot be determined; the observation of it is admittedly liable to … ‘errors of measurement’, but … this admittance is paramount to defining the acceleration per se as a parameter in a probability distribution — e.g., the mean value of a Gaussian distribution — and it is such parameters, not the observed estimates, which are assumed to follow the multiplicative law [acceleration = force / mass, or mass * acceleration = force].

“Thus, in any case an actual observation can be taken as nothing more than an accidental response, as it were, of an object — a person, a solid body, etc. — to a stimulus — a test, an item, a push, etc. — taking place in accordance with a potential distribution of responses — the qualification ‘potential’ referring to experimental situations which cannot possibly be [exactly] reproduced.

“In the cases considered [earlier in the book] this distribution depended on one relevant parameter only, which could be chosen such as to follow the multiplicative law.

“Where this law can be applied it provides a principle of measurement on a ratio scale of both stimulus parameters and object parameters, the conceptual status of which is comparable to that of measuring mass and force. Thus, … the reading accuracy of a child … can be measured with the same kind of objectivity as we may tell its weight …” (Rasch, 1960, p. 115).

Rasch’s model not only sets the parameters for data sufficient to the task of measurement, it lays out the relationships that must be found in data for objective results to be possible. Rasch studied with Ronald Fisher in London in 1935, expanded his understanding of statistical sufficiency with him, and then applied it in his measurement work, but not in the way that most statisticians understand it. Yes, in the context of group-level statistics, sufficiency concerns the reproducibility of a normal distribution when all that is known are the mean and the standard deviation. But sufficiency is something quite different in the context of individual-level measurement. Here, counts of correct answers or sums of ratings serve as sufficient statistics  for any statistical model’s parameters when they contain all of the information needed to establish that the parameters are independent of one another, and are not interacting in ways that keep them tied together. So despite his respect for Ronald Fisher and the concept of sufficiency, Rasch’s work with models and methods that worked equally well with many different kinds of distributions led him to jokingly suggest (Andersen, 1995, p. 385) that all textbooks mentioning the normal distribution should be burned!

In plain English, all that we’re talking about here is what Thurstone said: the ruler has to work the same way no matter what or who it is measuring, and we have to get the same results for what or who we are measuring no matter which ruler we use. When parameters are not separable, when they stick together because some measures change depending on which questions are asked or because some calibrations change depending on who answers them, we have encountered a “failure of invariance” that tells us something is wrong. If we are to persist in our efforts to determine if something objective exists and can be measured, we need to investigate these interactions and explain them. Maybe there was a data entry error. Maybe a form was misprinted. Maybe a question was poorly phrased. Maybe we have questions that address different constructs all mixed together. Maybe math word problems work like reading test items for students who can’t read the language they’re written in.  Standard statistical modeling ignores these potential violations of construct validity in favor of adding more parameters to the model.

But that’s another story for another time. Tomorrow we’ll take a closer look at sufficiency, in both conceptual and practical terms. Cited references are always available on request, but I’ll post them in a couple of days.

The “Standard Model,” Part II: Natural Law, Economics, Measurement, and Capital

At Tjalling Koopmans’ invitation, Rasch became involved with the Cowles Commission, working at the University of Chicago in the 1947 academic year, and giving presentations in the same seminar series as Milton Friedman, Kenneth Arrow, and Jimmie Savage (Linacre, 1998; Cowles Foundation, 1947, 1952; Rasch, 1953). Savage would later be instrumental in bringing Rasch back to Chicago in 1960.

Rasch was prompted to approach Savage about giving a course at Chicago after receiving a particularly strong response to some of his ideas from his old mentor, Frisch, when Frisch had come to Copenhagen to receive an honorary doctorate in 1959. Frisch shared the first Nobel Prize in economics with Tinbergen, was a co-founder, with Irving Fisher, of the Econometric Society,  invented words such as “econometrics” and “macro-economics,” and was the editor of Econometrica for many years. As recounted by Rasch (1977, pp. 63-66; also see Andrich, 1997; Wright, 1980, 1998), Frisch was struck by the disappearance of the person parameter from the comparisons of item calibrations in the series of equations he presented. In response to Frisch’s reaction, Rasch formalized his mathematical ideas in a Separability Theorem.

Why were the separable parameters  significant to Frisch? Because they addressed the problem that was at the center of Frisch’s network of concepts: autonomy, better known today as structural invariance (Aldrich, 1989, p. 15; Boumans, 2005, pp. 51 ff.; Haavelmo, 1948). Autonomy concerns the capacity of data to represent a pattern of relationships that holds up across the local particulars. It is, in effect, Frisch’s own particular way of extending the Standard Model. Irving Fisher (1930) had similarly stated what he termed a Separation Theorem, which, in the manner of previous work by Walras, Jevons, and others, was also presented in terms of a multiplicative relation between three variables. Frisch (1930) complemented Irving Fisher’s focus on an instrumental approach with a mathematical, axiomatic approach (Boumans, 2005) offering necessary and sufficient conditions for tests of Irving Fisher’s theorem.

When Rasch left Frisch, he went directly to London to work with Ronald Fisher, where he remained for a year. In the following decades, Rasch became known as the foremost advocate of Ronald Fisher’s ideas in Denmark. In particular, he stressed the value of statistical sufficiency, calling it the “high mark” of Fisher’s work (Fisher, 1922). Rasch’s student, Erling Andersen, later showed that when raw scores are both necessary and sufficient statistics for autonomous, separable parameters, the model employed is Rasch’s (Andersen, 1977; Fischer, 1981; van der Linden, 1992).

Whether or not Rasch’s conditions exactly reproduce Frisch’s, and whether or not his Separability Theorem is identical with Irving Fisher’s Separation Theorem, it would seem that time with Frisch exerted a significant degree of influence on Rasch, likely focusing his attention on statistical sufficiency, the autonomy implied by separable parameters, and the multiplicative relations of variable triples.

These developments, and those documented in previous of my blogs, suggest the existence of powerful and untapped potentials hidden within psychometrics and econometrics. The story told thus far remains incomplete. However compelling the logic and personal histories may be, central questions remain unanswered. To provide a more well-rounded assessment of the situation, we must take up several unresolved philosophical issues (Fisher, 2003a, 2003b, 2004).

It is my contention that, for better measurement to become more mainstream, a certain kind of cultural shift is going to have to happen. This shift has already been underway for decades, and has precedents that go back centuries. Its features are becoming more apparent as long term economic sustainability is understood to involve significant investments in humanly, socially and environmentally responsible practices.  For such practices to be more than just superficial expressions of intentions that might be less interested in the greater good than selfish gain, they have to emerge organically from cultural roots that are already alive and thriving.

It is not difficult to see how such an organic emergence might happen, though describing it appropriately requires an ability to keep the relationship of the local individual to the global universal always in mind. And even if and when that description might be provided, having it in hand in no way shows how it could be brought about. All we can do is to persist in preparing ourselves for the opportunities that arise, reading, thinking, discussing, and practicing. Then, and only then, might we start to plant the seeds, nurture them, and see them grow.

References

Aldrich, J. (1989). Autonomy. Oxford Economic Papers, 41, 15-34.

Andersen, E. B. (1977). Sufficient statistics and latent trait models. Psychometrika, 42(1), 69-81.

Andrich, D. (1997). Georg Rasch in his own words [excerpt from a 1979 interview]. Rasch Measurement Transactions, 11(1), 542-3. [http://www.rasch.org/rmt/rmt111.htm#Georg].

Boumans, M. (2001). Fisher’s instrumental approach to index numbers. In M. S. Morgan & J. Klein (Eds.), The age of economic measurement (pp. 313-44). Durham, North Carolina: Duke University Press.

Bjerkholt, O. (2001). Tracing Haavelmo’s steps from Confluence Analysis to the Probability Approach (Tech. Rep. No. 25). Oslo, Norway: Department of Economics, University of Oslo, in cooperation with The Frisch Centre for Economic Research.

Boumans, M. (1993). Paul Ehrenfest and Jan Tinbergen: A case of limited physics transfer. In N. De Marchi (Ed.), Non-natural social science: Reflecting on the enterprise of “More Heat than Light” (pp. 131-156). Durham, NC: Duke University Press.

Boumans, M. (2005). How economists model the world into numbers. New York: Routledge.

Burdick, D. S., Stone, M. H., & Stenner, A. J. (2006). The Combined Gas Law and a Rasch Reading Law. Rasch Measurement Transactions, 20(2), 1059-60 [http://www.rasch.org/rmt/rmt202.pdf].

Cowles Foundation for Research in Economics. (1947). Report for period 1947, Cowles Commission for Research in Economics. Retrieved 7 July 2009, from Yale University Dept. of Economics: http://cowles.econ.yale.edu/P/reports/1947.htm.

Cowles Foundation for Research in Economics. (1952). Biographies of Staff, Fellows, and Guests, 1932-1952. Retrieved 7 July 2009 from Yale University Dept. of Economics: http://cowles.econ.yale.edu/P/reports/1932-52d.htm#Biographies.

Fischer, G. H. (1981, March). On the existence and uniqueness of maximum-likelihood estimates in the Rasch model. Psychometrika, 46(1), 59-77.

Fisher, I. (1930). The theory of interest. New York: Macmillan.

Fisher, R. A. (1922). On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society of London, A, 222, 309-368.

Fisher, W. P., Jr. (1992). Objectivity in measurement: A philosophical history of Rasch’s separability theorem. In M. Wilson (Ed.), Objective measurement: Theory into practice. Vol. I (pp. 29-58). Norwood, New Jersey: Ablex Publishing Corporation.

Fisher, W. P., Jr. (2003a, December). Mathematics, measurement, metaphor, metaphysics: Part I. Implications for method in postmodern science. Theory & Psychology, 13(6), 753-90.

Fisher, W. P., Jr. (2003b, December). Mathematics, measurement, metaphor, metaphysics: Part II. Accounting for Galileo’s “fateful omission.” Theory & Psychology, 13(6), 791-828.

Fisher, W. P., Jr. (2004, October). Meaning and method in the social sciences. Human Studies: A Journal for Philosophy and the Social Sciences, 27(4), 429-54.

Fisher, W. P., Jr. (2007, Summer). Living capital metrics. Rasch Measurement Transactions, 21(1), 1092-3 [http://www.rasch.org/rmt/rmt211.pdf].

Fisher, W. P., Jr. (2008, March 28). Rasch, Frisch, two Fishers and the prehistory of the Separability Theorem. In Session 67.056. Reading Rasch Closely: The History and Future of Measurement. American Educational Research Association, Rasch Measurement SIG, New York University, New York City.

Frisch, R. (1930). Necessary and sufficient conditions regarding the form of an index number which shall meet certain of Fisher’s tests. Journal of the American Statistical Association, 25, 397-406.

Haavelmo, T. (1948). The autonomy of an economic relation. In R. Frisch &  et al. (Eds.), Autonomy of economic relations. Oslo, Norway: Memo DE-UO, 25-38.

Heilbron, J. L. (1993). Weighing imponderables and other quantitative science around 1800 Historical studies in the physical and biological sciences, 24 (Supplement), Part I, 1-337.

Jammer, M. (1999). Concepts of mass in contemporary physics and philosophy. Princeton, NJ: Princeton University Press.

Linacre, J. M. (1998). Rasch at the Cowles Commission. Rasch Measurement Transactions, 11(4), 603.

Maas, H. (2001). An instrument can make a science: Jevons’s balancing acts in economics. In M. S. Morgan & J. Klein (Eds.), The age of economic measurement (pp. 277-302). Durham, North Carolina: Duke University Press.

Mirowski, P. (1988). Against mechanism. Lanham, MD: Rowman & Littlefield.

Rasch, G. (1953, March 17-19). On simultaneous factor analysis in several populations. From the Uppsala Symposium on Psychological Factor Analysis. Nordisk Psykologi’s Monograph Series, 3, 65-71, 76-79, 82-88, 90.

Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests (Reprint, with Foreword and Afterword by B. D. Wright, Chicago: University of Chicago Press, 1980). Copenhagen, Denmark: Danmarks Paedogogiske Institut.

Rasch, G. (1977). On specific objectivity: An attempt at formalizing the request for generality and validity of scientific statements. Danish Yearbook of Philosophy,  14, 58-94.

van der Linden, W. J. (1992). Sufficient and necessary statistics. Rasch Measurement Transactions, 6(3), 231 [http://www.rasch.org/rmt/rmt63d.htm].

Wright, B. D. (1980). Foreword, Afterword. In Probabilistic models for some intelligence and attainment tests, by Georg Rasch (pp. ix-xix, 185-199. http://www.rasch.org/memo63.htm) [Reprint; original work published in 1960 by the Danish Institute for Educational Research]. Chicago, Illinois: University of Chicago Press.

Wright, B. D. (1994, Summer). Theory construction from empirical observations. Rasch Measurement Transactions, 8(2), 362 [http://www.rasch.org/rmt/rmt82h.htm].

Wright, B. D. (1998, Spring). Georg Rasch: The man behind the model. Popular Measurement, 1, 15-22 [http://www.rasch.org/pm/pm1-15.pdf].

Publications Documenting Score, Rating, Percentage Contrasts with Real Measures

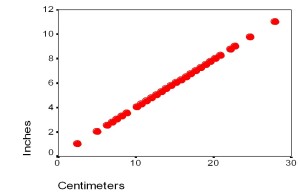
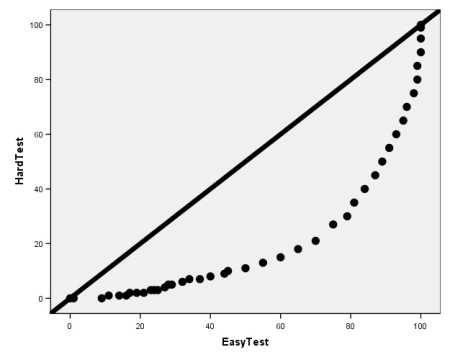
A few brief and easy introductions to the contrast between scores, ratings, and percentages vs measures include:

Linacre, J. M. (1992, Autumn). Why fuss about statistical sufficiency? Rasch Measurement Transactions, 6(3), 230 [http://www.rasch.org/rmt/rmt63c.htm].

Linacre, J. M. (1994, Summer). Likert or Rasch? Rasch Measurement Transactions, 8(2), 356 [http://www.rasch.org/rmt/rmt82d.htm].

Wright, B. D. (1992, Summer). Scores are not measures. Rasch Measurement Transactions, 6(1), 208 [http://www.rasch.org/rmt/rmt61n.htm].

Wright, B. D. (1989). Rasch model from counting right answers: Raw scores as sufficient statistics. Rasch Measurement Transactions, 3(2), 62 [http://www.rasch.org/rmt/rmt32e.htm].

Wright, B. D. (1993). Thinking with raw scores. Rasch Measurement Transactions, 7(2), 299-300 [http://www.rasch.org/rmt/rmt72r.htm].

Wright, B. D. (1999). Common sense for measurement. Rasch Measurement Transactions, 13(3), 704-5  [http://www.rasch.org/rmt/rmt133h.htm].

Longer and more technical comparisons include:

Andrich, D. (1989). Distinctions between assumptions and requirements in measurement in the social sciences. In J. A. Keats, R. Taft, R. A. Heath & S. H. Lovibond (Eds.), Mathematical and Theoretical Systems: Proceedings of the 24th International Congress of Psychology of the International Union of Psychological Science, Vol. 4 (pp. 7-16). North-Holland: Elsevier Science Publishers.

van Alphen, A., Halfens, R., Hasman, A., & Imbos, T. (1994). Likert or Rasch? Nothing is more applicable than good theory. Journal of Advanced Nursing, 20, 196-201.

Wright, B. D., & Linacre, J. M. (1989). Observations are always ordinal; measurements, however, must be interval. Archives of Physical Medicine and Rehabilitation, 70(12), 857-867 [http://www.rasch.org/memo44.htm].

Zhu, W. (1996). Should total scores from a rating scale be used directly? Research Quarterly for Exercise and Sport, 67(3), 363-372.

The following lists provide some key resources. The lists are intended to be representative, not comprehensive.  There are many works in addition to these that document the claims in yesterday’s table. Many of these books and articles are highly technical.  Good introductions can be found in Bezruczko (2005), Bond and Fox (2007), Smith and Smith (2004), Wilson (2005), Wright and Stone (1979), Wright and Masters (1982), Wright and Linacre (1989), and elsewhere. The www.rasch.org web site has comprehensive and current information on seminars, consultants, software, full text articles, professional association meetings, etc.

Books and Journal Issues

Andrich, D. (1988). Rasch models for measurement. Sage University Paper Series on Quantitative Applications in the Social Sciences, vol. series no. 07-068. Beverly Hills, California: Sage Publications.

Andrich, D., & Douglas, G. A. (Eds.). (1982). Rasch models for measurement in educational and psychological research [Special issue]. Education Research and Perspectives, 9(1), 5-118. [Full text available at www.rasch.org.]

Bezruczko, N. (Ed.). (2005). Rasch measurement in health sciences. Maple Grove, MN: JAM Press.

Bond, T., & Fox, C. (2007). Applying the Rasch model: Fundamental measurement in the human sciences, 2d edition. Mahwah, New Jersey: Lawrence Erlbaum Associates.

Choppin, B. (1985). In Memoriam: Bruce Choppin (T. N. Postlethwaite ed.) [Special issue]. Evaluation in Education: An International Review Series, 9(1).

DeBoeck, P., & Wilson, M. (Eds.). (2004). Explanatory item response models: A generalized linear and nonlinear approach. Statistics for Social and Behavioral Sciences). New York: Springer-Verlag.

Embretson, S. E., & Hershberger, S. L. (Eds.). (1999). The new rules of measurement: What every psychologist and educator should know. Hillsdale, New Jersey: Lawrence Erlbaum Associates.

Engelhard, G., Jr., & Wilson, M. (1996). Objective measurement: Theory into practice, Vol. 3. Norwood, New Jersey: Ablex.

Fischer, G. H., & Molenaar, I. (1995). Rasch models: Foundations, recent developments, and applications. New York: Springer-Verlag.

Fisher, W. P., Jr., & Wright, B. D. (Eds.). (1994). Applications of Probabilistic Conjoint Measurement [Special Issue]. International Journal of Educational Research, 21(6), 557-664.

Garner, M., Draney, K., Wilson, M., Engelhard, G., Jr., & Fisher, W. P., Jr. (Eds.). (2009). Advances in Rasch measurement, Vol. One. Maple Grove, MN: JAM Press.

Granger, C. V., & Gresham, G. E. (Eds). (1993, August). New Developments in Functional Assessment [Special Issue]. Physical Medicine and Rehabilitation Clinics of North America, 4(3), 417-611.

Linacre, J. M. (1989). Many-facet Rasch measurement. Chicago, Illinois: MESA Press.

Liu, X., & Boone, W. (2006). Applications of Rasch measurement in science education. Maple Grove, MN: JAM Press.

Masters, G. N. (2007). Special issue: Programme for International Student Assessment (PISA). Journal of Applied Measurement, 8(3), 235-335.

Masters, G. N., & Keeves, J. P. (Eds.). (1999). Advances in measurement in educational research and assessment. New York: Pergamon.

Osborne, J. W. (Ed.). (2007). Best practices in quantitative methods. Thousand Oaks, CA: Sage.

Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests (Reprint, with Foreword and Afterword by B. D. Wright, Chicago: University of Chicago Press, 1980). Copenhagen, Denmark: Danmarks Paedogogiske Institut.

Smith, E. V., Jr., & Smith, R. M. (Eds.) (2004). Introduction to Rasch measurement. Maple Grove, MN: JAM Press.

Smith, E. V., Jr., & Smith, R. M. (2007). Rasch measurement: Advanced and specialized applications. Maple Grove, MN: JAM Press.

Smith, R. M. (Ed.). (1997, June). Outcome Measurement [Special Issue]. Physical Medicine & Rehabilitation State of the Art Reviews, 11(2), 261-428.

Smith, R. M. (1999). Rasch measurement models. Maple Grove, MN: JAM Press.

von Davier, M. (2006). Multivariate and mixture distribution Rasch models. New York: Springer.

Wilson, M. (1992). Objective measurement: Theory into practice, Vol. 1. Norwood, New Jersey: Ablex.

Wilson, M. (1994). Objective measurement: Theory into practice, Vol. 2. Norwood, New Jersey: Ablex.

Wilson, M. (2005). Constructing measures: An item response modeling approach. Mahwah, New Jersey: Lawrence Erlbaum Associates.

Wilson, M., Draney, K., Brown, N., & Duckor, B. (Eds.). (2009). Advances in Rasch measurement, Vol. Two (p. in press). Maple Grove, MN: JAM Press.

Wilson, M., & Engelhard, G. (2000). Objective measurement: Theory into practice, Vol. 5. Westport, Connecticut: Ablex Publishing.

Wilson, M., Engelhard, G., & Draney, K. (Eds.). (1997). Objective measurement: Theory into practice, Vol. 4. Norwood, New Jersey: Ablex.

Wright, B. D., & Masters, G. N. (1982). Rating scale analysis: Rasch measurement. Chicago, Illinois: MESA Press.

Wright, B. D., & Stone, M. H. (1979). Best test design: Rasch measurement. Chicago, Illinois: MESA Press.

Wright, B. D., & Stone, M. H. (1999). Measurement essentials. Wilmington, DE: Wide Range, Inc. [http://www.rasch.org/memos.htm#measess].

Key Articles

Andersen, E. B. (1977). Sufficient statistics and latent trait models. Psychometrika, 42(1), 69-81.

Andrich, D. (1978). A rating formulation for ordered response categories. Psychometrika, 43, 561-73.

Andrich, D. (2002). Understanding resistance to the data-model relationship in Rasch’s paradigm: A reflection for the next generation. Journal of Applied Measurement, 3(3), 325-59.

Andrich, D. (2004, January). Controversy and the Rasch model: A characteristic of incompatible paradigms? Medical Care, 42(1), I-7–I-16.

Beltyukova, S. A., Stone, G. E., & Fox, C. M. (2008). Magnitude estimation and categorical rating scaling in social sciences: A theoretical and psychometric controversy. Journal of Applied Measurement, 9(2), 151-159.

Choppin, B. (1968). An item bank using sample-free calibration. Nature, 219, 870-872.

Embretson, S. E. (1996, September). Item Response Theory models and spurious interaction effects in factorial ANOVA designs. Applied Psychological Measurement, 20(3), 201-212.

Engelhard, G. (2008, July). Historical perspectives on invariant measurement: Guttman, Rasch, and Mokken. Measurement: Interdisciplinary Research & Perspectives, 6(3), 155-189.

Fischer, G. H. (1973). The linear logistic test model as an instrument in educational research. Acta Psychologica, 37, 359-374.

Fischer, G. H. (1981, March). On the existence and uniqueness of maximum-likelihood estimates in the Rasch model. Psychometrika, 46(1), 59-77.

Fischer, G. H. (1989). Applying the principles of specific objectivity and of generalizability to the measurement of change. Psychometrika, 52(4), 565-587.

Fisher, W. P., Jr. (1997). Physical disability construct convergence across instruments: Towards a universal metric. Journal of Outcome Measurement, 1(2), 87-113.

Fisher, W. P., Jr. (2004, October). Meaning and method in the social sciences. Human Studies: A Journal for Philosophy and the Social Sciences, 27(4), 429-54.

Fisher, W. P., Jr. (2009, July). Invariance and traceability for measures of human, social, and natural capital: Theory and application. Measurement (Elsevier), in press.

Grosse, M. E., & Wright, B. D. (1986, Sep). Setting, evaluating, and maintaining certification standards with the Rasch model. Evaluation & the Health Professions, 9(3), 267-285.

Hall, W. J., Wijsman, R. A., & Ghosh, J. K. (1965). The relationship between sufficiency and invariance with applications in sequential analysis. Annals of Mathematical Statistics, 36, 575-614.

Kamata, A. (2001, March). Item analysis by the Hierarchical Generalized Linear Model. Journal of Educational Measurement, 38(1), 79-93.

Karabatsos, G., & Ullrich, J. R. (2002). Enumerating and testing conjoint measurement models. Mathematical Social Sciences, 43, 487-505.

Linacre, J. M. (1997). Instantaneous measurement and diagnosis. Physical Medicine and Rehabilitation State of the Art Reviews, 11(2), 315-324.

Linacre, J. M. (2002). Optimizing rating scale category effectiveness. Journal of Applied Measurement, 3(1), 85-106.

Lunz, M. E., & Bergstrom, B. A. (1991). Comparability of decision for computer adaptive and written examinations. Journal of Allied Health, 20(1), 15-23.

Lunz, M. E., Wright, B. D., & Linacre, J. M. (1990). Measuring the impact of judge severity on examination scores. Applied Measurement in Education, 3/4, 331-345.

Masters, G. N. (1985, March). Common-person equating with the Rasch model. Applied Psychological Measurement, 9(1), 73-82.

Mislevy, R. J., Steinberg, L. S., & Almond, R. G. (2003). On the structure of educational assessments. Measurement: Interdisciplinary Research and Perspectives, 1(1), 3-62.

Pelton, T., & Bunderson, V. (2003). The recovery of the density scale using a stochastic quasi-realization of additive conjoint measurement. Journal of Applied Measurement, 4(3), 269-81.

Rasch, G. (1961). On general laws and the meaning of measurement in psychology. In Proceedings of the fourth Berkeley symposium on mathematical statistics and probability (pp. 321-333 [http://www.rasch.org/memo1960.pdf]). Berkeley, California: University of California Press.

Rasch, G. (1966). An individualistic approach to item analysis. In P. F. Lazarsfeld & N. W. Henry (Eds.), Readings in mathematical social science (pp. 89-108). Chicago, Illinois: Science Research Associates.

Rasch, G. (1966, July). An informal report on the present state of a theory of objectivity in comparisons. Unpublished paper [http://www.rasch.org/memo1966.pdf].

Rasch, G. (1966). An item analysis which takes individual differences into account. British Journal of Mathematical and Statistical Psychology, 19, 49-57.

Rasch, G. (1968, September 6). A mathematical theory of objectivity and its consequences for model construction. [Unpublished paper [http://www.rasch.org/memo1968.pdf]], Amsterdam, the Netherlands: Institute of Mathematical Statistics, European Branch.

Rasch, G. (1977). On specific objectivity: An attempt at formalizing the request for generality and validity of scientific statements. Danish Yearbook of Philosophy, 14, 58-94.

Romanoski, J. T., & Douglas, G. (2002). Rasch-transformed raw scores and two-way ANOVA: A simulation analysis. Journal of Applied Measurement, 3(4), 421-430.

Smith, R. M. (1996). A comparison of methods for determining dimensionality in Rasch measurement. Structural Equation Modeling, 3(1), 25-40.

Smith, R. M. (2000). Fit analysis in latent trait measurement models. Journal of Applied Measurement, 1(2), 199-218.

Stenner, A. J., & Smith III, M. (1982). Testing construct theories. Perceptual and Motor Skills, 55, 415-426.

Stenner, A. J. (1994). Specific objectivity – local and general. Rasch Measurement Transactions, 8(3), 374 [http://www.rasch.org/rmt/rmt83e.htm].

Stone, G. E., Beltyukova, S. A., & Fox, C. M. (2008). Objective standard setting for judge-mediated examinations. International Journal of Testing, 8(2), 180-196.

Stone, M. H. (2003). Substantive scale construction. Journal of Applied Measurement, 4(3), 282-97.

Wilson, M., & Sloane, K. (2000). From principles to practice: An embedded assessment system. Applied Measurement in Education, 13(2), 181-208.

Wright, B. D. (1968). Sample-free test calibration and person measurement. In Proceedings of the 1967 invitational conference on testing problems (pp. 85-101 [http://www.rasch.org/memo1.htm]). Princeton, New Jersey: Educational Testing Service.

Wright, B. D. (1977). Solving measurement problems with the Rasch model. Journal of Educational Measurement, 14(2), 97-116 [http://www.rasch.org/memo42.htm].

Wright, B. D. (1980). Foreword, Afterword. In Probabilistic models for some intelligence and attainment tests, by Georg Rasch (pp. ix-xix, 185-199. http://www.rasch.org/memo63.htm). Chicago, Illinois: University of Chicago Press.

Wright, B. D. (1984). Despair and hope for educational measurement. Contemporary Education Review, 3(1), 281-288 [http://www.rasch.org/memo41.htm].

Wright, B. D. (1985). Additivity in psychological measurement. In E. Roskam (Ed.), Measurement and personality assessment. North Holland: Elsevier Science Ltd.

Wright, B. D. (1996). Comparing Rasch measurement and factor analysis. Structural Equation Modeling, 3(1), 3-24.

Wright, B. D. (1997, June). Fundamental measurement for outcome evaluation. Physical Medicine & Rehabilitation State of the Art Reviews, 11(2), 261-88.

Wright, B. D. (1997, Winter). A history of social science measurement. Educational Measurement: Issues and Practice, 16(4), 33-45, 52 [http://www.rasch.org/memo62.htm].

Wright, B. D. (1999). Fundamental measurement for psychology. In S. E. Embretson & S. L. Hershberger (Eds.), The new rules of measurement: What every educator and psychologist should know (pp. 65-104 [http://www.rasch.org/memo64.htm]). Hillsdale, New Jersey: Lawrence Erlbaum Associates.

Wright, B. D., & Bell, S. R. (1984, Winter). Item banks: What, why, how. Journal of Educational Measurement, 21(4), 331-345 [http://www.rasch.org/memo43.htm].

Wright, B. D., & Linacre, J. M. (1989). Observations are always ordinal; measurements, however, must be interval. Archives of Physical Medicine and Rehabilitation, 70(12), 857-867 [http://www.rasch.org/memo44.htm].

Wright, B. D., & Mok, M. (2000). Understanding Rasch measurement: Rasch models overview. Journal of Applied Measurement, 1(1), 83-106.

Model Applications

Adams, R. J., Wu, M. L., & Macaskill, G. (1997). Scaling methodology and procedures for the mathematics and science scales. In M. O. Martin & D. L. Kelly (Eds.), Third International Mathematics and Science Study Technical Report: Vol. 2: Implementation and Analysis – Primary and Middle School Years. Boston: Center for the Study of Testing, Evaluation, and Educational Policy.

Andrich, D., & Van Schoubroeck, L. (1989, May). The General Health Questionnaire: A psychometric analysis using latent trait theory. Psychological Medicine, 19(2), 469-485.

Beltyukova, S. A., Stone, G. E., & Fox, C. M. (2004). Equating student satisfaction measures. Journal of Applied Measurement, 5(1), 62-9.

Bergstrom, B. A., & Lunz, M. E. (1999). CAT for certification and licensure. In F. Drasgow & J. B. Olson-Buchanan (Eds.), Innovations in computerized assessment (pp. 67-91). Mahwah, New Jersey: Lawrence Erlbaum Associates, Inc., Publishers.

Bond, T. G. (1994). Piaget and measurement II: Empirical validation of the Piagetian model. Archives de Psychologie, 63, 155-185.

Bunderson, C. V., & Newby, V. A. (2009). The relationships among design experiments, invariant measurement scales, and domain theories. Journal of Applied Measurement, 10(2), 117-137.

Cavanagh, R. F., & Romanoski, J. T. (2006, October). Rating scale instruments and measurement. Learning Environments Research, 9(3), 273-289.

Cipriani, D., Fox, C., Khuder, S., & Boudreau, N. (2005). Comparing Rasch analyses probability estimates to sensitivity, specificity and likelihood ratios when examining the utility of medical diagnostic tests. Journal of Applied Measurement, 6(2), 180-201.

Dawson, T. L. (2004, April). Assessing intellectual development: Three approaches, one sequence. Journal of Adult Development, 11(2), 71-85.

DeSalvo, K., Fisher, W. P. Jr., Tran, K., Bloser, N., Merrill, W., & Peabody, J. W. (2006, March). Assessing measurement properties of two single-item general health measures. Quality of Life Research, 15(2), 191-201.

Engelhard, G., Jr. (1992). The measurement of writing ability with a many-faceted Rasch model. Applied Measurement in Education, 5(3), 171-191.

Engelhard, G., Jr. (1997). Constructing rater and task banks for performance assessment. Journal of Outcome Measurement, 1(1), 19-33.

Fisher, W. P., Jr. (1998). A research program for accountable and patient-centered health status measures. Journal of Outcome Measurement, 2(3), 222-239.

Fisher, W. P., Jr., Harvey, R. F., Taylor, P., Kilgore, K. M., & Kelly, C. K. (1995, February). Rehabits: A common language of functional assessment. Archives of Physical Medicine and Rehabilitation, 76(2), 113-122.

Heinemann, A. W., Gershon, R., & Fisher, W. P., Jr. (2006). Development and application of the Orthotics and Prosthetics User Survey: Applications and opportunities for health care quality improvement. Journal of Prosthetics and Orthotics, 18(1), 80-85 [http://www.oandp.org/jpo/library/2006_01S_080.asp].

Heinemann, A. W., Linacre, J. M., Wright, B. D., Hamilton, B. B., & Granger, C. V. (1994). Prediction of rehabilitation outcomes with disability measures. Archives of Physical Medicine and Rehabilitation, 75(2), 133-143.

Hobart, J. C., Cano, S. J., O’Connor, R. J., Kinos, S., Heinzlef, O., Roullet, E. P., C., et al. (2003). Multiple Sclerosis Impact Scale-29 (MSIS-29):  Measurement stability across eight European countries. Multiple Sclerosis, 9, S23.

Hobart, J. C., Cano, S. J., Zajicek, J. P., & Thompson, A. J. (2007, December). Rating scales as outcome measures for clinical trials in neurology: Problems, solutions, and recommendations. Lancet Neurology, 6, 1094-1105.

Lai, J., Fisher, A., Magalhaes, L., & Bundy, A. C. (1996). Construct validity of the sensory integration and praxis tests. Occupational Therapy Journal of Research, 16(2), 75-97.

Lee, N. P., & Fisher, W. P., Jr. (2005). Evaluation of the Diabetes Self Care Scale. Journal of Applied Measurement, 6(4), 366-81.

Ludlow, L. H., & Haley, S. M. (1995, December). Rasch model logits: Interpretation, use, and transformation. Educational and Psychological Measurement, 55(6), 967-975.

Markward, N. J., & Fisher, W. P., Jr. (2004). Calibrating the genome. Journal of Applied Measurement, 5(2), 129-41.

Massof, R. W. (2007, August). An interval-scaled scoring algorithm for visual function questionnaires. Optometry & Vision Science, 84(8), E690-E705.

Massof, R. W. (2008, July-August). Editorial: Moving toward scientific measurements of quality of life. Ophthalmic Epidemiology, 15, 209-211.

Masters, G. N., Adams, R. J., & Lokan, J. (1994). Mapping student achievement. International Journal of Educational Research, 21(6), 595-610.

Mead, R. J. (2009). The ISR: Intelligent Student Reports. Journal of Applied Measurement, 10(2), 208-224.

Pelton, T., & Bunderson, V. (2003). The recovery of the density scale using a stochastic quasi-realization of additive conjoint measurement. Journal of Applied Measurement, 4(3), 269-81.

Smith, E. V., Jr. (2000). Metric development and score reporting in Rasch measurement. Journal of Applied Measurement, 1(3), 303-26.

Smith, R. M., & Taylor, P. (2004). Equating rehabilitation outcome scales: Developing common metrics. Journal of Applied Measurement, 5(3), 229-42.

Solloway, S., & Fisher, W. P., Jr. (2007). Mindfulness in measurement: Reconsidering the measurable in mindfulness. International Journal of Transpersonal Studies, 26, 58-81 [http://www.transpersonalstudies.org/volume_26_2007.html].

Stenner, A. J. (2001). The Lexile Framework: A common metric for matching readers and texts. California School Library Journal, 25(1), 41-2.

Wolfe, E. W., Ray, L. M., & Harris, D. C. (2004, October). A Rasch analysis of three measures of teacher perception generated from the School and Staffing Survey. Educational and Psychological Measurement, 64(5), 842-860.

Wolfe, F., Hawley, D., Goldenberg, D., Russell, I., Buskila, D., & Neumann, L. (2000, Aug). The assessment of functional impairment in fibromyalgia (FM): Rasch analyses of 5 functional scales and the development of the FM Health Assessment Questionnaire. Journal of Rheumatology, 27(8), 1989-99.

LivingCapitalMetrics Blog by William P. Fisher, Jr., Ph.D. is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License.
Based on a work at livingcapitalmetrics.wordpress.com.
Permissions beyond the scope of this license may be available at http://www.livingcapitalmetrics.com.

W

endt, A., & Tatum, D. S. (2005). Credentialing health care professionals. In N. Bezruczko (Ed.), Rasch measurement in health sciences (pp. 161-75). Maple Grove, MN: JAM Press.

Graphic Illustrations of Why Scores, Ratings, and Percentages Are Not Measures, Part One

It happens occasionally when I’m speaking to a group unfamiliar with measurement concepts that my audiences audibly gasp at some of the things I say. What can be so shocking about anything as mundane as measurement? A lot of things, in fact, since we are in the strange situation of having valid and rigorous intuitions about what measures ought to be, while we simultaneously have entire domains of life in which our measures almost never live up to those intuitions in practice.

So today I’d like to spell out a few things about measurement, graphically. First, I’m going to draw a picture of what good measurement looks like. This picture will illustrate why we value numbers and want to use them for managing what’s important. Then I’m going to draw a picture of what scores, ratings, and percentages look like. Here we’ll see how numbers do not automatically stand for something that adds up the way they do, and why we don’t want to use these funny numbers for managing anything we really care about. What we will see here, in effect, is why high stakes graduation, admissions, and professional certification and licensure testing agencies have long since abandoned scores, ratings, and percentages as their primary basis for making decisions.

After contrasting those pictures, a third picture will illustrate how to blend the valid intuitions informing what we expect from measures with the equally valid intuitions informing the observations expressed in scores, ratings, and percentages.

Imagine measuring everything in the room you’re in twice, once with a yardstick and once with a meterstick. You record every measure in inches and in centimeters. Then you plot these pairs of measures against each other, with inches on the vertical axis and centimeters on the horizontal. You would come up with a picture like Figure 1, below.

Figure 1. How We Expect Measures to Work

The key thing to appreciate about this plot is that the amounts of length measured by the two different instruments stay the same no matter which number line they are mapped onto. You would get a plot like this even if you sawed a yardstick in half and plotted the inches read off the two halves. You’d also get the same kind of a plot (obviously) if you paired up measures of the same things from two different manufacturer’s inch rulers, or from two different brands of metersticks. And you could do the same kind of thing with ounces and grams, or degrees Fahrenheit and Celsius.

So here we are immersed in the boring-to-the-point-of-being-banal details of measurement. We take these alignments completely for granted, but they are not given to us for nothing. They are products of the huge investments we make in metrological standards. Metrology came of age in the early nineteenth century. Until then, weights and measures varied from market to market. Units with the same name might be different sizes, and units with different names might be the same size. As was so rightly celebrated on World Metrology Day (May 20), metric uniformity contributes hugely to the world economy by reducing transaction costs and by structuring representations of fair value.

We are in dire need of similar metrological systems for human, social, and natural capital. Health care reform, improved education systems, and environmental management will not come anywhere near realizing their full potentials until we establish, implement, and monitor metrological standards that bring intangible forms of capital to economic life.

But can we construct plots like Figure 1 from the numeric scores, ratings, and percentages we commonly assume to be measures? Figure 2 shows the kind of picture we get when we plot percentages against each other (scores and ratings behave in the same way, for reasons given below). These data might be from easy and hard halves of the same reading or math test, from agreeable and disagreeable ends of the same rating scale survey, or from different tests or surveys that happen to vary in their difficulty or agreeability. The Figure 2 data might also come from different situations in which some event or outcome occurs more frequently in one place than it does in another (we’ll go more into this in Part Two of this report).

Figure 2. Percents Correct or Agreement from Different Tests or Surveys

In contrast with the linear relation obtained in the comparison of inches and centimeters, here we have a curve. Why must this relation necessarily be curved? It cannot be linear because both instruments limit their measurement ranges, and they set different limits. So, if someone scores a 0 on the easy instrument, they are highly likely to also score 0 on the instrument posing more difficult or disagreeable questions. Conversely, if someone scores 100 on the hard instrument, they are highly likely to also score 100 on the easy one.

But what is going to happen in the rest of the measurement range? By the definition of easy and hard, scores on the easy instrument will be higher than those on the hard one. And because the same measured amount is associated with different ranges in the easy and hard score distributions, the scores vary at different rates (Part Two will explore this phenomenon in more detail).

These kinds of numbers are called ordinal because they meaningfully convey information about rank order. They do not, however, stand for amounts that add up. We are, of course, completely free to treat these ordinal numbers however we want, in any kind of arithmetical or statistical comparison. Whether such comparisons are meaningful and useful is a completely different issue.

Figure 3 shows the Figure 2 data transformed. The mathematical transformation of the percentages produces what is known as a logit, so called because it is a log-odds unit, obtained as the natural logarithm of the response odds. (The response odds are the response probabilities–the original percentages of the maximum possible score–divided by one minus themselves.) This is the simplest possible way of estimating linear measures. Virtually no computer program providing these kinds of estimates would employ an algorithm this simple and potentially fallible.

Figure 3. Logit (Log-Odds Units) Estimates of the Figure 2 Data

Although the relationship shown in Figure 3 is not as precise as that shown in Figure 1, especially at the extremes, the values plotted fall far closer to the identity line than the values in Figure 2 do. Like Figure 1, Figure 3 shows that constant amounts of the thing measured exist irrespective of the particular number line they happen to be mapped onto.

What this means is that the two instruments could be designed so that the same numbers are read off of them when the same amounts are measured. We value numbers as much as we do because they are so completely transparent: 2+2=4 no matter what. But this transparency can be a liability when we assume that every unit amount is the same as all the others and they actually vary substantially. When different units stand for different amounts, confusion reigns. But we can reasonably hope and strive for great things as we bring human, social, and natural capital to life via universally uniform metrics traceable to reference standards.

A large literature on these methods exists and ought to be more widely read. For more information, see http://www.rasch.org, http://www.livingcapitalmetrics.com, etc.

LivingCapitalMetrics Blog by William P. Fisher, Jr., Ph.D. is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License.
Based on a work at livingcapitalmetrics.wordpress.com.
Permissions beyond the scope of this license may be available at http://www.livingcapitalmetrics.com.

What We Measure Matters

This comment was posted in reply to Chris Conley’s recent blog athttp://www.huffingtonpost.com/chip-conley/what-we-measure-matters_b_204676.html.

Right on, Chip!

The focus on meaning is essential. And unbeknownst to just about everyone but geeks like me, there is an extensive, longstanding, and mathematically rigorous scientific literature on meaningfulness in measurement.

We need to follow through from meaningful content to meaningful numbers, since survey and assessment ratings, scores, and response percentages are NOT measures in the everyday sense of what we mean when we deal with weight scales, clocks, thermometers, or rulers. That is, these numbers do not and cannot stand for something that adds up in the same way they do. The meaning of any given unit difference changes depending on where it falls in the measurement range, on who is measured, and/or on which item(s) are measuring.

For something we want to measure to be mapped onto a number line and to be truly and fully quantified, data have to have certain properties, like additivity, sufficiency, invariance, separable parameters, etc. When those properties are obtained, an instrument can be calibrated, data volume dramatically reduced, data quality assessed in terms of its internal consistency, and the measures made meaningfully interpretable.

Fortunately, scientific scaling methods have been applied in high stakes graduation, admissions, and professional certification/licensure testing for almost 40 years. Over the last 30 years, they have come to be applied in all kinds of survey research in health care and management consulting. Contact me for more information, see my web site at www.livingcapitalmetrics.com, or see www.rasch.org for full text articles.
More on Happiness
Read the Article at HuffingtonPost